Parellelepiped, Tetrahedron Volume Calculator
Calculates the volumes of parallelepiped and tetrahedron for given vertices.
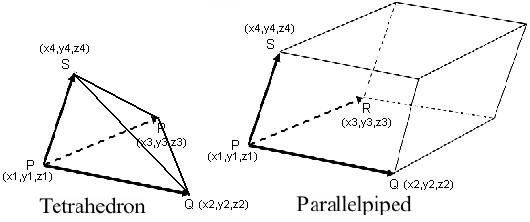
The tetrahedron is a regular pyramid.
Volume of a Parallelepiped :
Geometrically, the absolute value of the triple product represents the volume of the parallelepiped whose edges are the three vectors that meet in the same vertex.
Formula of volume is :
The volume of tetrahedron is :
$$ \text{Tetrahedron volume} = \frac{ \text{Parallelepiped volume (V)}} {6}$$
Formula of volume is :
$$ V=(x4-x1) \times [{(y2-y1) \times (z3-z1)}-{(z2-z1) \times (y3-y1)}]; $$
$$+ (y4-y1) \times [{ (z2-z1) \times (x3-x1)}-{(x2-x1) \times (z3-z1)}]; $$
$$+ (z4-z1) \times [{ (x2-x1) \times (y3-y1)}-{(y2-y1) \times (x3-x1) }]; $$
Volume of a Tetrahedron :
The volume of a tetrahedron is equal to 1/6 of the absolute value of the triple product.
The tetrahedron has four faces which are equilateral triangles and has 6 edges in regular tetrahedron having equal in length, the regular tetrahedron has four vertices and 3 faces meets at any one of vertex.The volume of tetrahedron is :
$$ \text{Tetrahedron volume} = \frac{ \text{Parallelepiped volume (V)}} {6}$$
